About two years ago, I started hearing a lot about "deep learning" and a powerful algorithm called a neural network. These things seem to be everywhere: from Siri and to facial recognition. I must admit, somewhat embarrassingly, it took me quite some time to figure out what exactly a neural network was.
Everything that I read, when trying to understand the Neural Network, suffered from one of two problems. Some pieces just weren't that technical, and described the analogy of his algorithm to a human brain. They talked about things called "hidden layers" without telling me what was actually going on in them. The other type of post had a lot of math very quickly. It's not that I couldn't understand the math, but I wanted the high-level summary technical summary, knowing I would work through the math later.
Everything that I read, when trying to understand the Neural Network, suffered from one of two problems. Some pieces just weren't that technical, and described the analogy of his algorithm to a human brain. They talked about things called "hidden layers" without telling me what was actually going on in them. The other type of post had a lot of math very quickly. It's not that I couldn't understand the math, but I wanted the high-level summary technical summary, knowing I would work through the math later.
But, two things became very clear. First, these the "blackest box" of the machine learning algorithms we have. Everything about inference and decision-making in the last post does not apply when using the NNs. Second, they are really really powerful. They are extraordinarily good at addressing some of the toughest data science problems. Given their recent success, they aren't going anywhere.
So it was time to learn!
This blog-post gets somewhat technical fairly quickly, but I am going to try to focus on the intuition of the neural network more than the math. However, if you are not familiar with any statistics or math, you may need to follow some of the links I provide. And, Unlike every other blog I read about neural networks, I am not really going describe the analogy to brain. I don't really know enough about how the brain works and I don't think the description is all that illuminating.
Instead, I want to begin by describing briefly one of the most basic algorithms used across statistics: the logistic regression. A logistic curve is an S-shaped curve that ranges between zero and one, getting closer and closer to those boundaries near the extremes. It has the following equation:
Because the curve fits between zero and one, data scientists frequently use it to fit to a probability. When using a logistic regression, a data-scientist loads a whole bunch of data,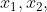 
(the features) to identify the best-fit 
(the betas), to estimate the probability of some target variable. The betas form the exact shape of the curve, like how steep it is or where it intersects the y-axis. These betas also tell us something about the importance of each variable; they are the impact that each feature has on the probability (actually, the log-odds). This algorithm is one of the work-horses of statistics and data-science. It's nice because the curve is simple, the betas have a clear meaning, and using linear algebra a data-scientist can identify statistical significance.
However, it has one big downside. Look carefully at that term in parenthesis. It's the equation for a line!Which roughly speaking, means this formula is linear in nature, the probability is a function of a linear combination of the input data. This means the logistic function is quite good at predicting blue and orange points when the data looks like this. The separation between the colors in linear.
But, it would do much worse with this. Because the relationship is circular, or quadratic.
To overcome this, researchers in machine learning have found that combinations of models tend to do better than a single model when it comes to classification or prediction. These are called ensemble methods. I won't get into the details here, but it's actually not all that hard to understand the intuition. When I said before that a data scientist is trying to find the "best-fit" betas, most of the time there is no way to ensure that the betas are actually the best fit.* There are things we do to try and make sure its close. So if any one model can be wrong, why not make a whole lot of models, each randomly a little different from each other, and have them vote?
My interpretation is that this this mostly a what a neural network is. It's a whole bunch of logistic regressions, the outputs of which feed into another logistic regression making the prediction.
Neural Networks
This is the classic picture of a neural network. A networks is a series of nodes (the circles) and edges (the lines that connect them).
But, this picture actually kind of obscures what is going on, so I am going to talk through it.
On the lefthand side, is what is called the input layer. These nodes represent the raw data themselves, the x's in the logistic equation above, or the positions of the circles on the two graphs.
The next layer, which is usually referred to as the hidden-layer, and is a very different type of node. Each node is a logistic function, taking some linear combination of the inputs, and producing that score between zero and one. And then all the way on the right, they are all feeding back into yet another logistic function. That is, we have a logistic regression of the logistic regressions to produce the final output. Each edge is the associated weight, or the betas for that particular logistic regression.
So, roughly speaking, if you understand logistic regression, you understand what neural-network is doing.
Of course, when I said "roughly speaking", I mean that intuition is very very rough. First of all, these don't actually need to be logistic function, they can be other similar functions. Similarly, the output doesn't need to be a logistic function. For example, if you are predicting a continuous variable, it could just be linear regression. Or there can be multiple output notes, so each logistic regression in the hidden layer can feed into multiple output regressions.
Second, the model contains one more type of node that I didn't describe previously: the bias term. Running all these separate logistic regressions would have no value if they were all very similar to each other. So, the NN forces some randomness into the system, in the form of that first beta term. Instead of letting the algorithm find the beta, the neural-network randomly assigns an intercept (usually between -1 and 1). Because each of the logistic regression in the hidden layer has a different intercept, all other betas will be different too. They are best fit, conditional on the random beta. To represent this in the network, we have a bunch of nodes which are equal to one. They also have an associated weight for each of the regression nodes they feed into, which is the intercept and these weights never change (I'll describe that more very soon!).
The third reason this was very roughly speaking, is that there is no reason to constrain a neural network to one hidden layer. Very often often, you'll see neural networks with 2, 3, or even more hidden layers. At first, I thought my analogy of ensemble logistic regressions would cease to make sense with more hidden layers. Then I realized something else, if having a whole bunch of slightly random logistic functions vote creates better predictions than one logistic regression (the 1 hidden layer neural), why wouldn't weighting a whole bunch of those create a better predictions than just 1 of those. Each hidden layer is just weighting some other ensemble of neural-networks before that (each of which is just a weighted set of logistic regressions).
Back Propagation
The fourth, and final reason my analogy above was only "roughly speaking" is because the logistic regression story leaves out how you find all the betas (or weights) which create the best prediction. The algorithm for this called back prorogation. If you've been doing statistics, optimization, or machine-learning for a while, its a relatively simple algorithm. But if this is all new to you, it can be a little intimidating, as there is linear algebra and calculus involved.
I am going to try to explain this without math, but its going to be tough so bear with me. Many machine learning algorithms use a method called gradient descent, to find the best fit betas. Very roughly speaking, this algorithm is equivalent to a person standing on the top of a hill, in the middle of a hilly landscape, and trying to find the lowest point as quickly as possible. An approximate way to find the lowest point is to look around, find the steepest direction, take one step in that direction, and do it again. This is only approximate, while it doesn't guarantee that the person standing at the top of the hill find the lowest point in the whole landscape, it does generally guarantee they will get to a place where they can't take a lower step. This is how a logistic regressions work in the world of big-data (with smaller data sets, neater solutions using linear algebra exist, but they can be very computationally expensive).
Why does this relate to the neural network? Every machine learning algorithm has this thing called a loss function. The loss function is the sum the difference between the predicted values coming out of a regression their actual values. Actually to be technically correct, with is the sum of the squares. The goal is to make that sum as small as possible: the lowest point in the hilly landscape. When a computer begins fitting a machine learning algorithm, it takes some random numbers, the equivalent of being plopped down randomly in that hilly landscape. Then it finds the steepest direction (using calculus, this is finding a derivative) and takes a step.
So, the true beauty of the neural network, is the realization that the computer can iteratively solve the gradient descent problem through all of the logistic regression. It can find the best step to take at the output layer node. And because of the chain rule (if you remember you calculus). It took me a couple of tries to find a summary of back-propagation that I found relatively easy to follow, here's a link to my favorite.
I won't repeat all the math here, but I will try to provide the some of the intuition of training a neural network. There are essentially three steps
1. initialize the network with random weights
2. forward propagate, by solving each of the node values, for a given set of inputs and a given sets of weights.
3. Update the weights, but solving for the gradient of each node. Solving the gradient of each node, requires taking the derivative of the loss function for the output node. Then for each prior node in the network, taking the weighted sum of the derivatives of the following nodes, multiplied by the derivative a current node. I personally liked the description provided in slide 16 of the slide above.
Also I have some code that shows it here.
Why use a neural network?
Neural networks are used because they are really good at predictions and classification. But, that's a bit of an simplification, because other algorithms are also really good. In my understanding, Neural Networks can buy the user two, related things. First, they can handle non-linearities really well. If you think about it, a single layered neural network is just a logistic regression, and that can handle a linear relationship. But a logistic regression with a single hidden layer, is a linear combination of a bunch of lines. With 3 nodes in the hidden layer you can make a triangle, with 4 you can make a square. Then with two hidden layers, with multiple nodes, you can start combining those shapes. Point is, the more hidden layers and the more nodes in those layers, the more crazy combination of those lines you can create, such that the shape doesn't resemble lines at all. I found this amazing tool, (which I can't take any credit for) that really helped me understand this intuition. I love playing with this thing, it's like watching a lava lamp, walk through iterations of gradient decent and seeing new shapes form. Mousing over each node shows how lines are being combined.
Second, when a data scientists don't know how to summarize your data, the neural network can do it for you. That is, each of these nodes serves as statistical summary of your data. In the world of logistic regression, identifying these statistical summaries that serve as representations of relationships of real world phenomena is generally referred to as feature engineering. This requires taking data, and somehow transforming it in ways will provide some signal and is the process of creating a large number of hypotheses about which inputs are related to the target variable. When they are all mixed together in a machine learning algorithm, it will squeeze as much signal out of these hypotheses as possible to make an efficient prediction. Data Scientists who understand the context of the problem, and the physical or social phenomena that underly the relationship between the input and the output data will be better suited to create these predictions.
One of the cool things about neural networks is that the seem to automate this process. Each node in the hidden layer, can be thought of as a feature in feeding into the output layer. Thus, something like a time series of data, pixels in a picture, or words in a document, will be combined into some summary each node of the hidden layer, which supplies predicted power to the output layer. This is really good for problems where we don't really know how to generate features, like pixels in a picture. But on the other hand, in many many cases, we have these features in the nodes in the hidden layers, but still don't have any good interpretation of them.
Neural Networks as Feature Engineering
Obviously, recent advances are showing that neural networks have incredible potential for solving some of the hardest data science problems. But, given the content of my previous post, it will come as no surprise that I am more interested in learning something about structural relationships in the data, than I am about purely creating the best prediction possible. In a couple of cases, researchers have figured out how to make the features the true value of the network.
A great example of this is the word2vec algorithm (this is one great explanation of this). Very roughly speaking, word2vec trains nueral network using a corpus of text. The prediction the network is making is somewhat incidental, but you can think of it as whether a n-gram (a set n words) would ever appear together in a corpus of text. So the input layer has n nodes, one for each word, and the ouput layer is simply a classification of whether the n-gram appears in the corpus, and semantically valid** There is only a single hidden layer but it iss very wide, on the order of the 300 nodes. Each of these nodes represents a latent a feature, or dimension of the word. The prediction itself is never used, but the 300 dimensional space characterizing each word is incredibly valuable; it lets users build analogies. For example, gender could be encoded in these dimensions, and if you were to think about where each word appears in the 300 dimensional space, "king" and "queen" would have the same offset as "man" and "woman". So the nodes are latent features with information about the words themselves, derived from the content of the corpus, and the relatively fake prediction it was used for (here's a much better description of word2vec)
On the other hand, even though neural-networks are often described as a general algorithm for learning, it turns out some of the most effective neural networks impose a structure that comes from some level of domain expertise, not unlike feature engineering. The clearest example of this I have seen is convolutional neural networks which are really good at image recognition. Rather than having networks where all the input nodes have connections to all the hidden layers, there are hidden layers that connect only certain inputs, generally pixels near one another. At the same time, the weights across nodes in the hidden layer are constrained to be the same, essentially replicating the same feature for subsections of the image. These networks make use of both convolution layers, where the same pixels can be used in multiple hidden neurons and pooling layers, in each each pixel feeds to only one layer. In essence these restriction are trying to help the network do things like detect edges in am image, or control for various orientations of the image. While the features themselves may be difficult to interpret, understanding how information is frequently encoded in pictures, and restricting the network accordingly makes it more powerful, not less. In my mind, this is a form of feature engineering.
Are Neural Networks AI?
I think one of the reasons why Neural Networks have captured so much popular press right now, is they some how feel like we are approaching AI. Their very name makes us think that we have written code that makes computers act like a brain. And they fact that each node can be interpreted as a feature means that the algorithm is taking on some of the more hypothesis driven research that a data scientist does. And they are good at inherently human task, like language and image recognition.
But I am skeptical of all that. They are very very cool statistical algorithms that are breaking through solving some of the hardest data science problems. But I suspect, over-time, we will start to identify they types of questions they are good at answering and they types of questions they are bad at answering. And fundamentally, they are useful at classifying data. They tend to be good at classifying data with a structure, but a pretty difficult to decipher structure. And while these are important capabilities at making smarter machines, I am not sure there is anything about them that is fundamentally "smarter" or more sentient than any other algorithm we have .
** Again, a simplification
No comments:
Post a Comment